Postulate 0->Newpde




click on pink titles below for backup physics:
Postulate 0 gives Newpde psi and other psi properties
Part III hybrid states (eg.,metric quantization from goo=koo)
Rest Miscellaneous






Figure 1 solves the puzzle of physics and real#math (just postulate 0) and figure 1 below explains why.
(Ockam’s razor motivated) Postulate 0 <->Physics :
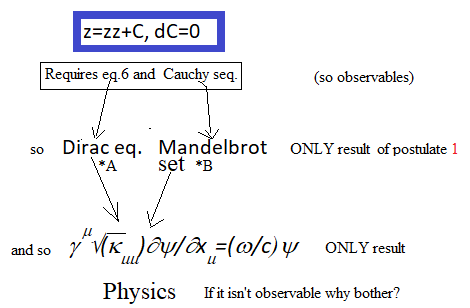
Mandelbrot Set Plug in the left side (of eq.1) z into the right side zz repeatedly and use δC=0 and get the Mandelbrot set iteration formula.The Mandelbrot set CM is (and from the postulated δCM=0), zN+1=zNzN+CM (since δ(z’-zz)=δ(zN+1-zNzN)= δ(∞-∞)=0). (the z=zz) z=0=zo. Fiegenbaum point CM smallest real line Mandelbulb on next smaller (baseline) scale. Mandelbulb areas (drdt) for smallest Clifford algebra extremum drdt.


Boost m1=tau+mu+me=3e from S=½ to L=1 at stable r=rH, 2P3/2 with m1/2=mp reduced mass. See above sect.2 of above postulate 1 file for some more applications. See PartI, partII, PartIII for the rest.
Comparison and contrast with mainstream concerns:
The origin of the many postulates of quantum mechanics is considered to be a mystery by one and all.
Not really: 1) Quantum mechanics arises from a circle.(see below)
The connection between general relativity and quantum mechanics is stated over and over again to be the greatest unsolved problem in physics.
Not really: 2) General Relativity(GR) comes out of quantum mechanics in 1 step.(see below)
A century has been devoted to the origin of high energy particle physics by thousands of people using billions of dollars worth of particle accelerators. It is supposed to be quarks, gluons, qcd SU(3) gauge forces, require many free parameters,..and so on and so forth.
Not really: 3) (high energy 3e composite) Particle physics is just a ortho and para state (see below)
The latest version “Standard electroweak Model” is now encumbered by pages of Lagrangian density terms, and so literally hundreds of postulates.
Not really: 4) Rotate e,v to get the Standard electroweak Model (it’s merely composite e,v). (see below)
Expansion of the above answers:
(1)Plug z=1+δz into z=zz+C, δC=0 (eq.1) and get δ(δz+δzδz)=0 which splits into Im Clifford Algebra and Real Minkowski metric components which imply that circle ds2=dr2+dt2 so δz=dseiA. Write in angle ‘A’ radian measure dependence on r,t, take the r partial derivative and rearrange and you get a Hermitian operator and so “observables” formalism and then the Dirac equation of quantum mechanics (given that Clifford algebra). See sect.1 of above postulate 1 file.
(2) Note square roots of koo=1-rH/r=1/krr in the new pde (so same kij math functionality as in the Schwarzschild metric gij but coming from QM instead.). So squaring (actually iterating) the New pde on the next higher(cosmological) fractal scale, where rH=2GM/c2, gets the Schwarzchild metric gij of GR, a one step derivation. General relativity comes out of quantum mechanics in one simple step!
(3) The two positrons in 2P3/2 on the r=rH shell are moving rapidly, the central electron is not moving so much at the center, and this New pde 2P3/2 state is stable because of h/e flux quantization(PartII) and r=rH motion. So a Clebsch Gordon two body analysis with Paschen Back effect excitation, in a straightforward way, leads to a ortho(s,c,b) and para(t) states with ground state(u/d), the proton. Use Frobenius series solutions (Ch.9) individually for each of the s,c,b,t associated Nucleonic doublets (eg.,P,N for u/d) to get the particle multiplets. See PartII also.
4) The 4 axis (New pde) e,v rotations (giving consecutively the 4 Bosons: Zo,W+,W-,photon) at r=rH on the r,t plane are implied by eq.7 (also see appendix A). We even get Maxwell’s and Proca’s equations in these iterative rotations through the New pde e,v solutions which means taking a first derivative at each 45deg. rotation.
Conclusion: Ultimate Okcam’s razor postulate 1 implies math AND physics. We finally figured it out.